In this tutorial, I will walk you through how a quantum computer can break the RSA cryptogsystem, a widely-used public key algorithm. The following points will be discussed:

• Recall the RSA algorithm
• Quantum computers and their principles
• Shor’s quantum algorithm and how it could break RSA

A Brief Recap of RSA Cryptosystem

RSA cryptosystem, introduced by Rivest, Shamir, Adleman in 1977, is the first public key cryptosystem. It has been widely using in many applications in real world such as establishing a secure communication over an insecure channel, digtally signing a digital document, etc.

The RSA encryption consists of three (3) algorithms:

Key Generation

• Choose at random two big safe prime numbers $p$ and $q$. They must be kept secret.
• Public keys: two elements: the modulus $N = p \times q$ and a small public exponent $e$, often $e = 2^{16} + 1 = 65 537$. The length of $N$ should comply to up-to-date recommandations, for example, the current recommendation is using $128$-bit security level, that is equivalent to $3072$ bits of $N$.
• Private keys: two primes $p, q$, and a private exponent $d \equiv e^{-1} \bmod \lambda(N)$, where $\lambda$ is Carmichael’s totient function. All these values must be kept secret.

Note: The public keys can be freely distributed, as it is used for encryption or signature verification.

Encryption

Given a message $m$, its ciphertext is $c = m^e \pmod N$.

Decryption:

Given a ciphertext $c$, the private key’s owner recover the message $m = c^d \pmod N$.

Note: The plain RSA scheme depicted above is insecure against a number of attacks. To make it secure, the message must be formatted under randomized padding schemes such as OAEP or RSA-PSS.

RSA is secure because the difficulty of factoring the product of two large prime numbers (the modulus $N$) forms the basis of its security. Breaking RSA by factoring large numbers into their prime factors is believed computationally infeasible for sufficiently large key sizes.

What is Quantum Computer?

It started about 40 years ago with the academic papers of Richard P. Feynman Simulating Physics with Computers published on the International Journal of Theoretical Physics and Quantum Mechanical Computers published on the journal Foundations of Physics. In his papers, Manin scketched a theoretical foundation for quantum computing. The first paper is an abstract view on simulation of physics and what’s needed to deal with simulating quantum effects. The second paper is more details about what a quantum computer or quantum algorithm would actually look like.

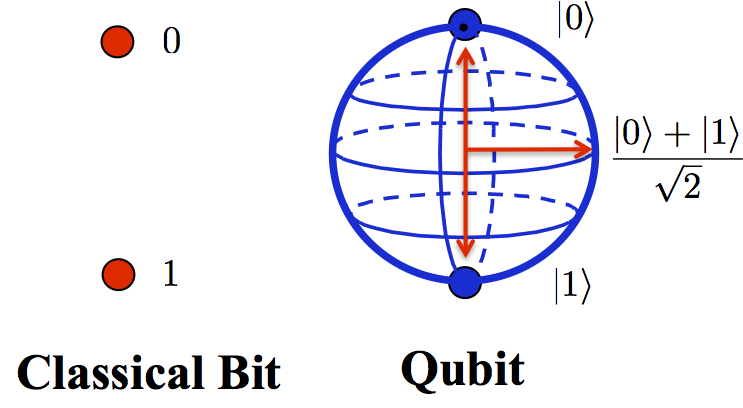
In a nutshell, quantum computers are built by applying the principles of quantum mechanics (superposition and entanglement) to perform operations on data. While the basic unit of information in a classical computer is a bit, which can be either a $0$ or a $1$, the basic unit in quantum computers is qubits.

• Superposition: qubits can exist in multiple states simultaneously (i.e., , it can be a $0$, a $1$, or both at the same time), allowing quantum computers to perform many calculations at the same time.
• Entanglement: this mechanism means the state of one qubit is directly related to the state of another, even if they are physically separated. This enables faster information transfer and processing.

The above unique properties of quantum mechanisms allow us to design quantum algorithms that could solve certain problems exponentially faster than classical computers.

How can a Quantum Computer break RSA?

By far, the RSA breaking record by using factorization algorithms with classical computers is RSA250, that is, $250$ decimal digits or $829$ binary digits of the modulus $N$ (see RSA Factoring Challenge). With the current NIST’s recommendations for using RSA-2048 or RSA-3072, users should not have any security concerns with classical computers.

However, 30 years ago (1994), Shor showed us a quantum algorithm that could theoretically break RSA in a polynomial time, that is, given a public modulus, Shor’s algorithm could easily find two prime factors $p$ and $q$ using a powerful quantum computer. So, how a quantum algorithm could break the RSA cryptosystem that the classical computers could not?

How a quantum computer works?

Let consider how a classical/quatum computer solve a tangible problem. For example, imagine you are the entrance of a maze and need to find the shortest path from the entrance to the exit of the maze. Each intersection in the maze, there will be two possible ways to go.

A typical solution you may think about is to search all possible paths, then make a comparison and conclude the shortest one. This kind of solution will run sequentially on a classical computer, that is, you enter the entrance, go to the first intersection, take the right way and continue this strategy until you reach to the exit or to a dead end. Either ways, you go back to find a next possible solution or another path to another dead end. The final solution will have once you visit all possible paths.

Let represent your choices at an intersection are $0$ or $1$, for example, $1$ if you choose right way and $0$ if you choose the left way. So, all path you have taken will be a binary chain, e.g., $11000100$. You also can represent the path with a dead end with a # at the end. The solution will be the chain with the least number of binary digits and without #. To obtain the solution, all possible paths must be visited and the time complexity will be $O(2^n)$, where $n$ is the number of the intersections.

Using quantum computers where we work with qubits. In a quantum state or superposition, those bits until they are measured, can be considered both $0$ or $1$ at the same time. This is similar to a spinning coin in which we don’t know it will be head or tail until it landed.

Let’s go back to the maze problem. Think quantum computer can think about multiple paths simultaneously. Once measured, it will show one path that we can verify its correctness easily. If that path was returned randomly the solution is is unlikely correct. However, in quantum computers, qubits can be arranged in ways that maximize the possibility of finding the correct path. This ability is what a quantum algorithm will provide us.

Shor’s Quantum Algorithm

Based on the Feynman’s quantum principles, Peter Shor developed the first quantum algorithm Algorithms for quantum computation: Discrete logarithms and factoring that can efficiently solve the factorization problem, which RSA cryptosystem relies on, and dicrete logarithm problem, which ElGamal cryptosystems and ECC relies on.

From wikipedia:

The problem that we are trying to solve is: given an odd composite number $N$, find its integer factors. To achieve this, Shor’s algorithm consists of two parts:

1. A classical reduction of the factoring problem to the problem of order-finding. This reduction is similar to that used for other factoring algorithms, such as the quadratic sieve.
2. A quantum algorithm to solve the order-finding problem.

Well, there are two parts in Shor’s algorithm. The first part works as usual as what the classical computers do and the second part: solving the order-finding or period finding problem is where a quantum computer can do a way better than a classical computer. Note that: efficiently solving the period finding problem is also the key point to efficiently solve the discrete-logarithm problem.

So, how Shor’s quantum algorithm efficiently solve the period finding problem. Let first recall some concepts.

Definition (Period Function): A function $f(x)$ is called periodic if there exists some non-zero value $r$ so that: \(f(x) = f(x + r),\) for all $x$ in the domain of $f(x)$, and $r$ will be called a period of the function $f(x)$.

Finding period

Shor applied a quantum Fourier transform (QFT) to find the period $r$. A classical computer can also find a period using the Fourier transform, however it will be generally computationally intensive. The key point in Shor’s quantum Fourier transform is that it operates on quantum states corresponding to different frequency components. Then, due to the principles of quantum superposition, the algorithm is able to process all possible frequencies simultaneously. This parallelism provides the potential exponential speedup over the classical Fourier transform.

Now, with a quantum computer, we know that the QFT can find a period of a function effectively. Let’s see how it will be applied in breaking the RSA cryptosystem.

Quantum Part

We first choose a number $a$ that is coprime with the modulus $N$ (i.e., no common factors with $N$ or $gcd(a, N) = 1$). To check if $a$ and $N$ are coprimes or not, we can use the Euclidean algorithm.

The goal of the quantum subroutine of Shor’s lgorithm is to find the order $r$ of the modulus $N$, which is the smallest positive integer such that:

With the Quantum Fourier Transform aforementioned, this period $r$ can be done retively easily by a quantum computer. Then, a period function $f_a$ is defined as:

Because of (1), we have:

So, the order $r$ when found will be the period of the function $f_a(x) = a^x \bmod N$.

Classical Part

As $r$ and $N$ are coprimes, from the euqation (1), we can see that $N$ divides $a^r - 1$, written $N \;|\; a^r - 1$. With a high probability (at least 50\%), the order $r$ returned from QFT subroutine is an even number, then using difference of squares, we have:

or, in the other words,

Because neither $a^{r/2} - 1$ nor $a^{r/2} + 1$ are multiple of $N$ and $a^{r/2} - 1 \equiv 0 \bmod N$ (as it would contradictorily imply that $r/2$ would be the order of $a$, which was already $r$). Thus, either $a^{r/2} - 1$ or $a^{r/2} + 1$ have a non-trivial common factor with $N$. This factor can be relatively easily calculate using the Euclidean algorithm:

$d = gcd(a^{r/2} - 1, N)$ or $d = gcd(a^{r/2} + 1, N)$, where $d \ne 1$. The found factor $d$ will be one of two primes $p$ or $q$ in the RSA key generation. The other secret prime can be found easily due to $N$ and $d$, that is $N/d \bmod N$.

Well, $p$ and $q$ were now recovered, that means the RSA cryptosystem was broken.

Note that: In case $r$ is odd number, we restart the QFT subroutine to get the new order $r$.

Complexity

The hardest part is to solve the finding period problem. QFT can do it in a polynomial time (that will be exponential time with a classical computer), thus the entire attack is in polynomial time with a quantum computer.