What happens in the trusted setup phase of the Groth16 protocol
Published:
The Groth16 Protocol
Groth16, probably the most wide-used zk-SNARK (Zero-Knowledge Succinct Non-Interactive Arguments of Knowledge) on blockchains, was introduced by Jens Groth at Eurocrypt 2016 (that’s why it is named groth16). The paper, entitled On the Size of Pairing-Based Non-interactive Arguments, could be on eprint/2016/260.
Groth16 is based on R1CS (Rank One Constraint Systems) arithmetization. While its proof consists of only 3 elliptic curve points, defined in the base filed $G_1$, the verification is also fast with only 3 pairing computations. Think if you implement the protocol with the BN curve for $128$-bit security level, the total size of 3 points in the proofs is about $200$ bytes ($3 \times 2 \times 254$ bits, each point represented by two 254-bit finite field elements). The below table was shown in the lecture ZKP MOOC Lecture 2: Overview of Modern SNARK Constructions comparing Groth16 to other zk-SNARKs.
| Size of proof | Verifier time | Setup | Post-quantum | |
|---|---|---|---|---|
| Groth16 | ~ 200 bytes ($\mathcal{O}_{\lambda}(1)$) | ~ 1.5 ms ($\mathcal{O}_{\lambda}(1)$) | Trusted per circuit (1) | No |
| Plonk | ~ 400 bytes ($\mathcal{O}_{\lambda}(1)$) | ~ 3 ms ($\mathcal{O}_{\lambda}(1)$) | Universal trusted setup (2) | No |
| Bulletproofs | ~ 1.5 Kbytes ($\mathcal{O}_{\lambda}(log |C|)$) | ~ 3 s ($\mathcal{O}_{\lambda}(|C|)$) | Transparent (3) | No |
| zk-STARK | ~ 100 Kbytes ($\mathcal{O}_{\lambda}(log^2 |C|)$) | ~ 10 ms ($\mathcal{O}_{\lambda}(log^2 |C|)$) | Transparent | Yes |
(1) Trusted per circuit requires the setup phase to run for every individual circuits, i.e., generating a Common Reference String (CRS) for one circuit; (2) Universal trusted setup runs only one time for all circuits; (3) Transparent requires nothing to setup.
The zk-SNARK protocols often require a trusted setup in order to generate a CRS (Common Reference String), proving and verification keys for prover and verifier, respectively. Compared to other protocol, Groth16 protocol requires trusted setup per circuit, that means, if you implement a new circuit, you must execute another trusted setup. Otherwise, it offers smaller proof size and faster verification, and these features probably makes this protocol more popular as it will consume less gas cost on Ethereum blockchain. Groth16 is suitable for applications generating many proofs for the same circuit and performance is crucial.
This article will discuss the two setup phases of the Groth16 protocol.
Gorth16 Setup Protocol
The trusted setup of the Groth16 protocol could be found in the page #17 of his paper. It is as the below picture:
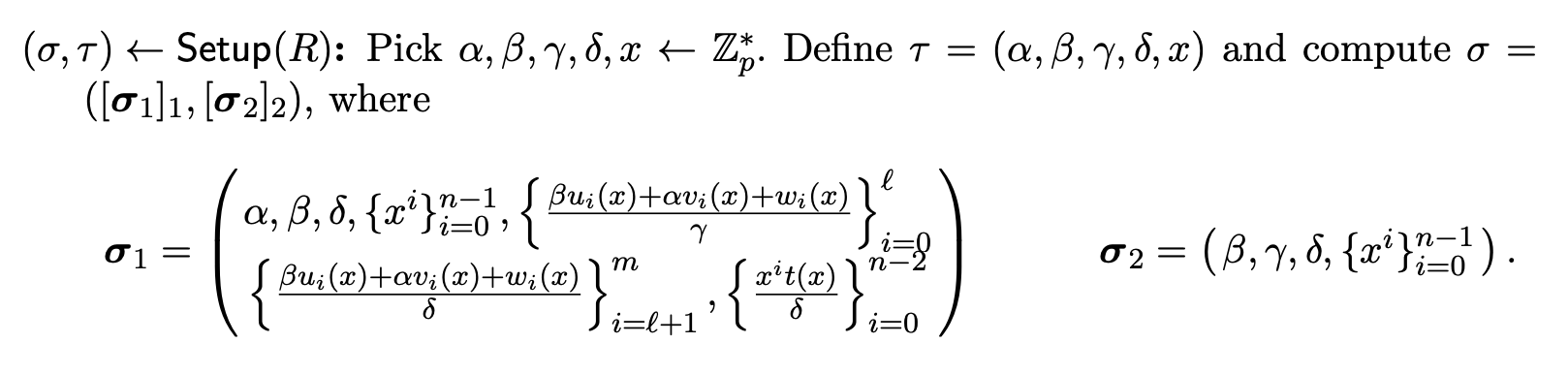
Universal Setup
Assume that you are working with a group of points $\mathbb{G}$ of order $p$ on an elliptic curve $E$ defined over a finite field $F_q$, and its generator $G$, i.e., $[p]G = \mathcal{0}$. This phase of setup will generate a random number $\tau$ and its powers $[\tau^0]G, [\tau^1]G, [\tau^2]G, …, [\tau^d]G$. These values could be used for any circuits. The reason for generating these values is for committing polynomials in the next steps of the protocol. For instance, to commit a polynomial $f(x) = \sum_{i = 0}^{d} a_i x^i$ without leaking coefficients, we will generate $com_f = f(\tau) \cdot G = a_0 + a_1 \cdot \tau \cdot G + a_2 \cdot \tau^2 \cdot G + \ldots + a_d \cdot \tau^d \cdot G \in \mathbb{G}$. This commitment is a point of $E$ (i.e., group element of $\mathbb{G}$) that could be considered as an encrypted version of $f(\tau)$ as long as we could not solve the discrete logarithm problem.
Note: You should remember that $p$ and $q$ are two distinct primes. For example, many practical ZKP systems use BN254 curve, in which:
$E: y^2 = x^3 + 3,$
$q = 21888242871839275222246405745257275088696311157297823662689037894645226208583$, and
$p = 21888242871839275222246405745257275088548364400416034343698204186575808495617$
The below simple python code demonstrate this phase 1 setup.
def generate_powers_of_tau(tau, degree, point):
return [multiply(point, int(tau ** i)) for i in range(degree + 1)]
"""
Trusted setup
Phase 1: setup for all circuits
"""
# 1. Get a random value tau
tau = random.randint(1, p)
# 2. Calculate tau*G1, tauˆ2*G1, ..., tauˆd*G1
powers_of_tau_for_G1 = generate_powers_of_tau(tau, d, G1)
# Calculate tau*G2, tauˆ2*G2, ..., tauˆd*G2
powers_of_tau_for_G2 = generate_powers_of_tau(tau, d, G2)
# Calculate powers of tau for evaluating h(x)t(x) at tau
t_tau = t_poly(tau)
powers_of_tau_for_ht = [multiply(powers_of_tau_for_G1[i], int(t_tau)) for i in range(d)]
As we are working with asymmetric pairing, we need to generate powers of tau for both points $G_1$ and $G_2$. The former is a generator in the base field $F_q$ and the later is the generator in the extension field $F_{q^k}$, where $k$ is the embedding degree of the elliptic curve $E$. For BN254 curve, $k = 12$. You must be familiar with pairing-friendly elliptic curves to understand that concept and to know why we need powers of tau in both fields. Generally speaking, a (Ate) pairing $e(Q, P)$ taking two points as parameters and return an element in the extension field $F_{q^k}$, where $Q$ and $P$ are multiple of $G_2$ and $G_1$, respectively. A complete introduction of such curves could be found in the paper A taxonomy of pairing-friendly elliptic curves by Freeman, Scott, and Teske.
The degree $d$ is the maximum degree of a polynomial that this powers of tau ceromony of a ZKP system will support for circuits. This number is equivalent to the maximum number of constraints of circuits. For example, snarkjs support a circuit with up to $2^{28}$ (≈256 million) constraints, so $d$ could be any number smaller than or equal to $2^{28}$.
Important: $\tau$ must be discarded after this setup phase to prevent dishonest provers from inventing fake ZK proofs without using the knowledge about the witness. Given powers of tau $[\tau]G_i, [\tau^2]G_i, …, [\tau^d]G_i$, for $i = 1, 2$, an adversary could not recover the value of $\tau$ unless he could solve the discrete logarithm problem, believed a NP-Complete problem, and hence infeasible to solve with the classical computers.
Circuit-Specific Setup
At this phase, assume you are working on a computation problem and converted it into a R1CS system that can be encoded as:
\[Lw \cdot Rw = Ow,\]where $L, R, O$ are matrices with $n$ rows (equal to the number of constraints) and $m$ columns (equal to the length of the witness), and $w$ is the witness vector. To understand step-by-step how to convert a computation problem to a R1CS system, the best online resource I found is The Rareskills Book of Zero Knowledge.
At the phase 2 setup per circuit, the trusted server generates random value $\alpha, \beta$ that will be used to prevent a potential cheating prover from making up three curve points of proof $A, B$, and $C$:
alpha = random.randint(1, p)
beta = random.randint(1, p)
alpha_G1 = multiply(G1, int(alpha)) # alpha*G1
beta_G1 = multiply(G1, int(beta)) # beta*G1
beta_G2 = multiply(G2, int(beta)) # beta*G2
Trusted server also generates random $\gamma$ and $\delta$ to prevent dishonest prover from forgeries with public inputs to generate a false proof:
gamma = random.randint(1, p)
gamma_G2 = multiply(G2, int(gamma)) # gamma*G2
gamma_inv = 1 / GFp(gamma) # should be defined in a finite field GF(p)
delta = random.randint(1, p)
delta_G1 = multiply(G1, int(delta)) # delta*G1
delta_G2 = multiply(G2, int(delta)) # delta*G2
delta_inv = 1 / GFp(delta)
Finally, trusted server compute powers of $\tau$ for public and private inputs
"""
Given three matrices L, R and O, generate powers of tau for public and private input,
i,e., C = beta*U + alpha*V + W
@:param d: degree of the polynomials formed from columns in the matrices, d = n - 1, where n = #rows
@:param m: #columns of the matrices = len(witness)
@:return two list of powers of tau (elliptic curve points):
- one related to public inputs (i.e., first l values in the witness vector) will be for verifier
- one related to private inputs (i.e, last m - l values in the witness vector) will be for prover
"""
def generate_powers_of_tau_for_inputs(powers_of_tau, d, m, L_mat, R_mat, O_mat, alpha, beta, ell, gamma_inv, delta_inv):
taus_for_public_inputs = []
taus_for_private_inputs = []
# require degree + 1 points to interpolate a polynomial of degree d
xs = Fp(np.array([i + 1 for i in range(d + 1)]))
# Each i-th col of matrices L, R, and W will be converted to a polynomial U_i(x), V_i(x) and W_i(x)
for i in range(m):
# U_i(x) = interpolate the i-th column of matrix L
poly_Ui = galois.lagrange_poly(xs, L_mat[:, i])
# Perform a random shift by multiplying the poly with a random factor beta
beta_Ui = poly_Ui * beta # multiply U with beta
# V_i(x) = interpolate the i-th column of matrix R
poly_Vi = galois.lagrange_poly(xs, R_mat[:, i])
# Perform a random shift by multiplying the poly with a random factor alpha
alpha_Vi = poly_Vi * alpha
# W_i(x) = interpolate the i-th column of matrix W
poly_Wi = galois.lagrange_poly(xs, O_mat[:, i])
sum_poly = beta_Ui + alpha_Vi + poly_Wi
if i < ell:
taus_for_public_inputs.append(inner_product(powers_of_tau, (sum_poly.coeffs[::-1]) * gamma_inv))
else:
taus_for_private_inputs.append(inner_product(powers_of_tau, (sum_poly.coeffs[::-1]) * delta_inv))
return taus_for_public_inputs, taus_for_private_inputs
taus_for_public_inputs, taus_for_private_inputs = \
generate_powers_of_tau_for_inputs(powers_of_tau_for_G1, d, m, L, R, O, alpha, beta, ell, gamma_inv, delta_inv)
Trusted Setup in practical ZKP systems
As mentioned above, the value of $\tau$ must be kept secret, it thus is risky if letting only a single entity to generate it. Practical ZKP systems usually implement a MPC (Multi-Party Computation) protocol for powers of tau. As there are many available online articles on this topic, I won’t talk more about this here. If you want to understand more, go to the following links:
Groth16 setup by snarkjs
Let’s see how snarkjs perform the trusted setup phase for the Groth16 protocol:
You may need to install snarkjs first
npm install -g snarkjs@latest
snarkjs is a javascript library that can generate ZK proofs and verify them. Inputs for snarkjs to generate proofs are r1cs files that could be generated from circom.
Start a new powers of tau ceremony
snarkjs ptn bn128 8 pot08_0000.ptau
or,
snarkjs powersoftau new bn128 8 pot08_0000.ptau
Parameters:
bn128: BN curve at 128-bit security level8: power of 2 indicating the maximum number of permitted constraints, i.e., this ceromony result will allow circuits with maximum $2^8$ constraintspot08_0000.ptau: output file
This command takes as input an elliptic curve (snarkjs supports bn128 and bls12-381), a number smaller than 28 (as snarkjs supports upto $2^{28}$ constraints only), and will output a transcript, i.e., powers of tau, individually generated by yourself.
Contribute to the ceremony
snarkjs ptc pot08_0000.ptau pot08_0001.ptau --name="First contribution"
or,
snarkjs powersoftau contribute pot08_0000.ptau pot08_0001.ptau --name="First contribution"
Parameters:
pot08_0000.ptau: input file that is the transcript so farpot08_0001.ptau: output a new transcript containing all challenges and responses that have been taken contribution so far--name="First contribution": a note as you want
As mentioned earlier, a powers of tau ceremony should be a multi-party computation protocol, that is, contributed by a number of contributors. This command takes as input a individual contribution, then includes it with other contributions so far to return a new transcript.
Per circuit setup
After having lists of powers of tau, you are now going to setup transcript for a specific circuit you have.
Phase 2 preparation
snarkjs pt2 pot08_0001.ptau pot08_final.ptau
or,
snarkjs powersoftau prepare phase2 pot08_0001.ptau pot08_final.ptau
Parameters:
pot08_0001.ptau: input file that is the transcript so farpot08_final.ptau: output a new transcript adding $\alpha$ and $\beta$ values
This step setups random values $\alpha$ and $\beta$ to prevent a dishonest prover from cheating as discussed above.
Setup proving and verification keys
Assume that you implemented a circuit and compiled it to get a r1cs file. If not, Circom can help with that. These links will guide you how to write and compile a circuit.
Assume your circuit compiled to a r1cs file and named circuit.r1cs. Use the below command to generate proving and verification keys for this circuit.
snarkjs g16s circuit.r1cs pot08_final.ptau circuit_0000.zkey
or,
snarkjs groth16 setup circuit.r1cs pot08_final.ptau circuit_0000.zkey
This command generates the reference zkey without phase 2 contributions. You then need to contribute to the phase 2 of the ceremony:
snarkjs zkc circuit_0000.zkey circuit_0001.zkey --name="1st Contributor Name"
or,
snarkjs zkey contribute circuit_0000.zkey circuit_0001.zkey --name="1st Contributor Name"
Finally, you export the verification key, making it accessible to verifiers:
snarkjs zkev circuit_0001.zkey verification_key.json
or,
snarkjs zkey export verificationkey circuit_0001.zkey verification_key.json
Closing
This tutorial discussed the trusted setup phase in the Groth’16 Zero-Knowledge Proof protocol. Some Python code were just demonstrated the setup process. You can find the full implementation of Groth16 protocol on this repo. Hope you find it fun and useful!
